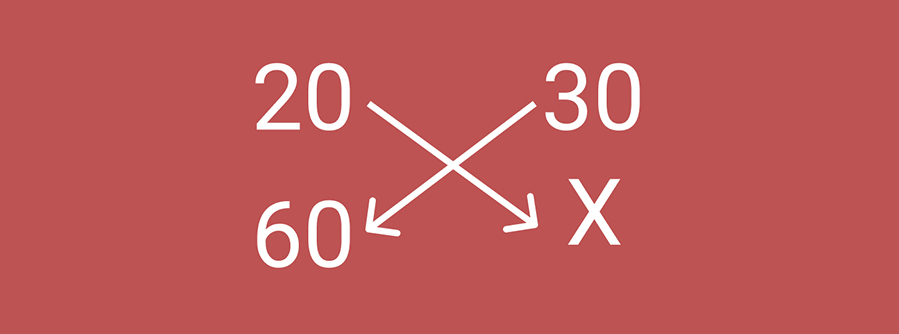A regra de três é um dos conteúdos básicos de Matemática mais importantes para os alunos. Grande parte dos exercícios de avaliações, como Enem, vestibulares e concursos, pode ser resolvida usando esse conhecimento, além disso, essa regra também pode ser aplicada a questões de Física, Química e também para resolver problemas cotidianos.

Por ser tão importante, reunimos os três erros cometidos com mais frequência na aplicação da regra de três para ajudar os alunos a não cometê-los mais e também para tirar possíveis dúvidas sobre esse conteúdo.

1 – Interpretação do problema

Esse erro não é cometido apenas na regra de três, mas nos conteúdos matemáticos em geral. É muito importante interpretar corretamente o texto dos problemas.

A partir do seguinte exemplo, observe como proceder nesse caso: Um automóvel faz uma viagem a 90 km/h e, em determinado período de tempo, consegue percorrer 270 km. Se esse mesmo automóvel estivesse a 120 km/h, quantos quilômetros percorreria a mais que o percorrido na primeira situação?

O primeiro passo para resolver um exercício desse tipo é perceber que o período de tempo em questão é irrelevante para os cálculos. Só importa que seja o mesmo período para as duas situações. Depois, perceba também que, para encontrar os quilômetros a mais que foram percorridos, devemos, primeiramente, encontrar o total de quilômetros percorridos a 120 km/h, ou seja, os cálculos precisam ser feitos em duas etapas.

Acontece que, ao finalizar a primeira etapa, alguns alunos acreditam ter terminado o problema e acabam por deixar a resolução incompleta. Observe a regra de três para a primeira etapa do exercício:

90 = 270
120 x

90x = 270·120

90x = 32400

x = 32400
90

x = 360 km

Como queremos saber quantos quilômetros a mais foram percorridos, devemos ainda calcular a diferença entre 360 e 270:

360 – 270 = 90 km

Assim, o automóvel terá percorrido 90 km a mais, a 120 km/h, no período de tempo indicado.

2 – Montagem da resolução

Toda regra de três pode ser compreendida como uma proporção, isto é, ela é a igualdade entre duas razões. Essas duas razões podem ser tiradas de figuras geométricas ou de situações como a do exemplo anterior e, para que realmente sejam iguais, precisam seguir uma determinada ordem.

Exemplo: Uma fábrica produz 150 unidades de um elemento por dia e, para isso, conta com 25 funcionários. Planejando uma ampliação da produção para 275 peças diárias, quantos funcionários serão necessários para produzi-las, considerando as condições ideais de trabalho?

A primeira razão que montaremos será referente à situação atual da indústria. A fração será formada por numerador = número de funcionário, e denominador = número de peças.

25
150

A segunda razão que montaremos é referente à situação pretendida pela empresa e deve seguir o mesmo padrão da inicial: número de funcionários no numerador e número de peças no denominador.

x
275

Como as duas razões foram montadas seguindo um padrão (correto), sabemos que os seus resultados serão iguais e, por isso, podemos escrever:

25 = x
150 275

Resolvendo a regra de três, temos:

150x = 25·275

x = 6875
150

x = 45,833…

Assim, serão necessários 46 funcionários.

3 – Grandezas direta ou inversamente proporcionais

Um dos erros mais frequentes na resolução de regra de três diz respeito a não verificar se as grandezas envolvidas são direta ou inversamente proporcionais. No primeiro caso, a regra de três é feita como nos dois exemplos anteriores. No segundo caso, não. Por isso, é necessária bastante atenção para não cometer esse tipo de erro.

Portanto, para considerar duas grandezas como diretamente proporcionais, devemos perceber que, ao aumentar os valores referentes a uma delas, os valores referentes a outra também aumentam. Caso contrário, as duas grandezas são inversamente proporcionais.

Exemplo: Um automóvel está a uma velocidade de 90 km/h e gasta 2 horas para percorrer determinado trajeto. Se esse automóvel estivesse a 45 km/h, quantas horas gastaria no mesmo trajeto?

Observe que, ao diminuir a velocidade do automóvel, o correto é entender que o tempo gasto no mesmo trajeto deverá aumentar. Sendo assim, as grandezas são inversamente proporcionais.

Para resolver esse tipo de regra de três, monte a proporção normalmente e, em seguida, inverta uma das razões antes de prosseguir:

90 = 2
45 x

90 = x
45 2

45x = 90·2

45x = 180

x = 180
45

x = 4 horas

Por Luiz Paulo Moreira, graduado em Matemática